こんにちは、ぱぱけん (@yi_ki411) です。
本記事では技術士第一次試験の基礎科目のうち、2群(情報・論理に関するもの)に特化して、出題内容の解説や勉強方法についてまとめています。
・基礎科目 2群の出題内容が知りたい
・2群の勉強方法と対策が知りたい
・2群の目標点を知りたい

技術士第一次試験に一発合格した筆者(@yi_ki411) が解説します。








2群の出題内容


まずは2群の出題内容を見てみましょう。
出題分野と問題形式
技術士第一次試験の基礎科目は「科学技術全般にわたる基礎知識」とされています。
その中でも2群は「情報・論理に関するもの」という分野から出題されます。
各群で共通ですが、6問出題され、3問を選択し解答します。
情報に関する問題では基数変換(n進法)、ビット・バイト計算、ICT・インターネット・情報セキュリティーに関する問題などが出題されます。
論理に関する問題では論理式、集合演算、アルゴリズム、構文図などが出題されます。
過去7年の出題内容
過去7年の2群の出題内容は下記のようになっています。
| 番号 | 令和4年度 | 令和3年度 | 令和2年度 | 令和元年度再 | 令和元年度 | 平成30年度 | 平成29年度 |
|---|---|---|---|---|---|---|---|
| 1 | テレワーク | 情報セキュリティ | 情報の圧縮 | 情報セキュリティ | 基数変換 | 情報セキュリティ | 情報セキュリティ |
| 2 | 集合 | 論理式 | 論理式 | アルゴリズム | 二分探索木 | 構文図 | 浮動小数点数 |
| 3 | アクセス時間 | バイト計算 | 標的型攻撃 | バイト計算 | ベクトル | 補数 | アルゴリズム |
| 4 | ハミング距離 | 数理論理 | 補数 | 浮動小数点数 | 数値列表現 | 論理式 | 数理論理 |
| 5 | アルゴリズム | 中置記法 | アルゴリズム | ベン図 | ハミング距離 | 中置記法 | 数値列表現 |
| 6 | ビット計算 | 漸近的記法 | 実行時間 | 写像 | スタック | 集合 | 実行時間 |
表のうち青字で示したものは計算問題です。
計算問題が多いですが、公式の暗記が必要だったり複雑な計算というのはあまりありません。
2群の出題キーワード


2群の出題内容をキーワードで整理します。
情報に関するもの
計算問題はやり方が決まっていますので、過去問を繰り返せばすぐになれると思います。
文章系の問題についてはほとんどが情報セキュリティに関する問題です。
計算問題
・基数変換(n進法)(解説はこちら)
・ビット計算、バイト計算
・実行時間、実効メモリアクセス(解説はこちら)
文章問題(暗記系)
・電子メール
・キャッシュ
・テレワーク(近年の新傾向)
・電子署名、公開鍵、秘密鍵
・WEP
・ウイルス対策、スパムメール
情報セキュリティーに関する問題については知っているか知らないかだけで正答を導けるかが決まります。
知識がない方にとってはいわゆる暗記系の問題ですが、常識的な問題も多いです。
最初から捨て問題にはせずまずは過去問に目を通してみましょう。
論理に関するもの
・論理式
・構文図、アルゴリズム、二分探索木、算術木
・浮動小数点数、固定小数点数
論理に関する問題は簡単な計算を必要とするものが多いです。
また、論理の分野ではありますが、基数変換(n進法)と合わせて出題がされることもあります。
例えば、アルゴリズムの問題では基数変換をフロー図で示す問題などがあります。
2群の勉強方法と対策


2群の問題は基数変換やビット計算、論理式など、計算手法を知らないと太刀打ちできないという特徴があります。
一方で、類似問題が多くやり方さえ覚えてしまえば簡単に解ける問題が多いです。
また、文章問題は過去問の引用が多く、他の群と同じく過去問を繰り返しこなすことも重要になってきます。
ここでは具体的な勉強方法と対策について解説します。
基数変換(n進法)をマスターする
基数変換(n進法)の問題はほぼ毎年のように出題されており、超頻出となっています。
単に基数変換を求めてくる問題もあれば、アルゴリズムの問題の中で基数変換が必要になる場合もあります。
2群で得点を確保するためには、普段から基数変換になじみがない方でも対策が必須です。
問題の形式や難易度は出題年によって変わりますが、やり方さえマスターしてしまえばある程度の問題は解けます。
n進法とは
n進法とは、n種の数字・記号を使って表す数の表現方法です。
・2進法は0,1の2種
・10進法は0,1,2,3,4,5,6,7,8,9の10種
・16進法は0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,Fの16種
技術士第一次試験では2進法、10進法、16進法が頻出となります。



私たちが日常生活でよく使っているのは10進法ですね。
n進法はn番目の数の次に位が繰り上がります。
・2進法では0,1の次が10
・10進法では9の次が10
・16進法ではFの次が10
2進法の表記と10進法の表記を並べてみましょう。


2進法では10進法の2で位が繰り上がっていますね。次は4で繰り上がり、次は8で繰り上がります。
2進法はこのように2のm乗で位が繰り上がるのが特徴です。
ちなみにコンピューターの内部では10進法ではなく2進法が使われています。コンピューターに内蔵されるCPUの電子回路では電気の流れで信号の判断をしており、流れているか流れていないかの状態を1と0で表現できる2進法のほうが都合がよいのです。
基数変換のやり方を覚えよう
技術士第一次試験では2進数と10進数の変換を問う問題が超頻出です。
ある数字の基数の変換を行うため、「基数変換」といいます。
10進数を2進数に変換する場合と、逆に2進数を10進数に変換する場合でやり方が異なるため、それぞれ解説します。
まず、10進数の218.52を下記のように分解します。
218.52=2・102+1・101+8・100+5・10-1+2・10-2
2進数も同じように分解できます。1001.01を分解してみましょう。
1001.01=1・23+0・22+0・21+1・20+0・2-1+1・2-2=8+0+0+1+0+0.25=9.25
となります。これが10進数への変換方法そのものです。
16進数の場合もやり方は同じです。下記のようにルールを覚えて下さい。
n進法のabcd.efを10進法に変換
abcd.ef=a・n3+b・n2+c・n1+d・n0+e・n-1+f・n-2
さきほどの逆です。218.52を2進数に変換してみましょう。
整数の部分と小数の部分を分けて計算を行います。
10進数の整数の部分は2で割っていくという作業をします。
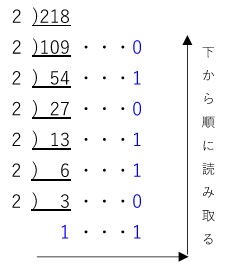

2で割るので余りが1か0のどちらかになります。余りを右に書いておきます。
余りを下から読み上げると「11011010」となります。
これが求める2進数の整数部分です。
次に、10進数の小数部分は2をかけていきます。


2をかけたときの整数部分を上から読み取ると「10000101・・・」となります。
これが求める2進数の小数部分です。
なお、この作業はキリがないので適当なところで切り捨てます。
以上より、10進数の218.52は2進数で表すと11011010.10000101となります。



難しい計算をしているわけではないので、何度か練習すればすぐにマスターできると思います。
ビット・バイト計算は慣れている人は選択、わからなければ捨てる
ビット・バイトに関する計算問題もよく出題されていますが、超頻出というわけではないです。
2進法の考えに近く、慣れていない方にとってはとっつきにくい分野かと思います。
過去問を解いて解説を読んでもわからない場合は、捨ててしまうのも手です。



ちなみに私はビット・バイト計算は捨てていました。馴染みがない・・・
実行時間、実効メモリアクセスの問題は得点源
CPU実行時間ともいいます。頻出です。
数字だけが変わった過去問の類似問題が出ていますので、まずは過去問をこなし、解き方を覚えましょう。
実効アクセス時間は下記の式を覚えておけば求めることができます。
実効アクセス時間=(キャッシュのアクセス時間×ヒット率)+(主記憶のアクセス時間×NFP)
NFP=1-ヒット率
過去問の例題を見てみましょう。
平成28年度2-4
アクセス時間が1.00[ns]のキャッシュとアクセス時間が100[ns]の主記憶からなる計算機システムがある。キャッシュのヒット率が95%のとき、このシステムの実効アクセス時間として最も近い値はどれか。ただしキャッシュのヒット率とは呼び出されたデータがキャッシュに入っている確率である。
①0.05[ns] ②0.95[ns] ③5.00[ns] ④5.95[ns] ⑤95.0[ns]
早速、さきほどの式を使います。
NFP=1-0.95=0.05(5%)
実効アクセス時間=(キャッシュのアクセス時間×ヒット率)+(主記憶のアクセス時間×NFP)
=1.00×0.95+100×0.05
=0.95+5
=5.95 (正答:④)
となります。実効アクセス時間の算出式さえ暗記してしまえば計算自体は簡単です。
論理式・論理演算・ベン図・集合演算は合わせて勉強する
頻出です。難解な問題は少ない印象です。
論理演算と集合演算は近い概念ですので、合わせて勉強しましょう。
論理式は肯定命題と否定命題およびその積と和で表された記号列のことをいいます。
論理式の計算では「ド・モルガンの法則」を覚えておくと簡単に解けるものがあります。
余裕のある方はぜひ覚えておきましょう。下記のサイトで詳しく解説されています。
集合演算はベン図を書いてイメージをしながら解きましょう。
アルゴリズム・構文図・探索木・算術木の問題は落ち着いて問題文と図を読み取る
これらの分野の問題は一見とっつきにくそうに見えますが、問題文をよく読み取れば簡単な問題が多いです。
アルゴリズム
下図のように、ある定義をフロー図で表現した問題が出題されます。
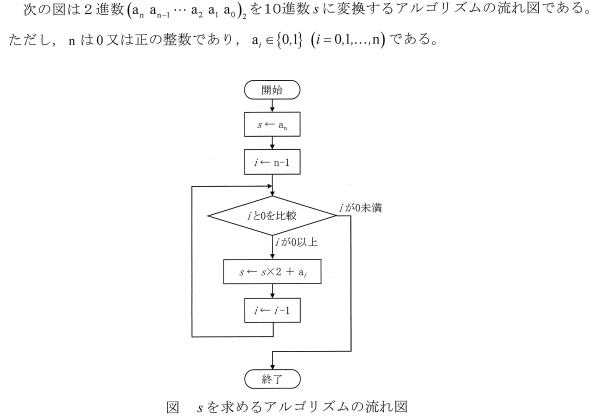

(過去問題(第一次試験)|公益社団法人 日本技術士会 (engineer.or.jp)より)
フロー(流れ)による繰り返し計算手法すなわちアルゴリズムです。
一見難しそうに見えますが、落ち着いて問題の条件をよく読み取り、フローに落とし込んでいくことで正答が導けます。
構文図
アルゴリズムに少し似ていますが、ある構文(ルール)を図式化したものです。
図式内の空欄を埋める問題がよく出ます。
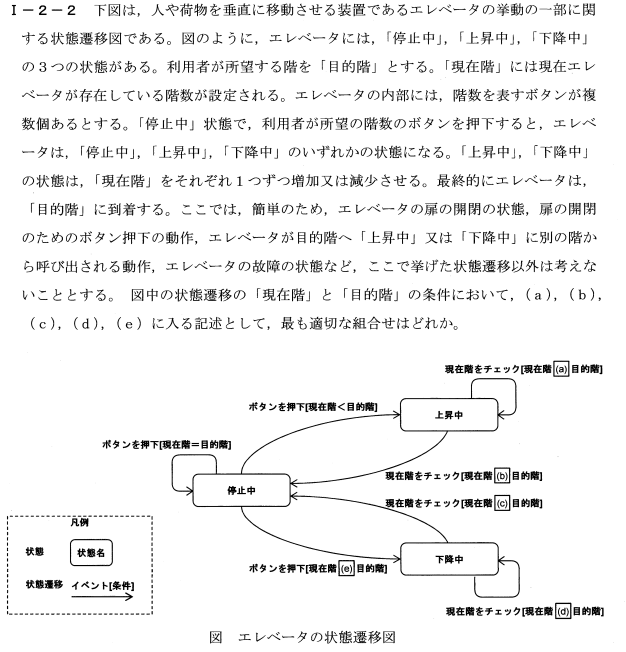

(過去問題(第一次試験)|公益社団法人 日本技術士会 (engineer.or.jp)より)
二分探索木・算術木
探索木、算術木は数式を図式化したものです。
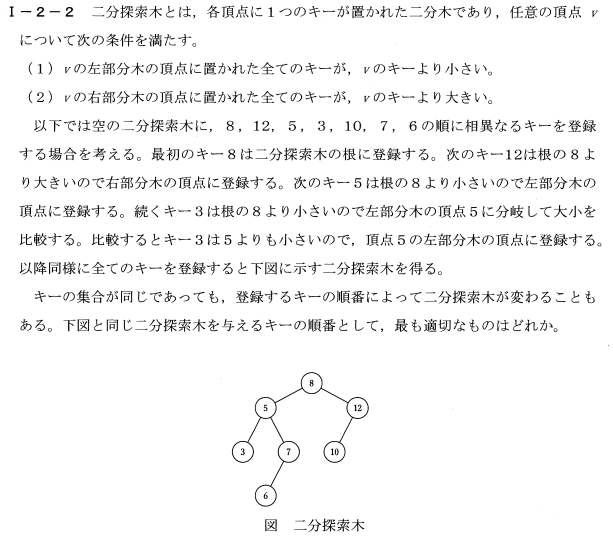

(過去問題(第一次試験)|公益社団法人 日本技術士会 (engineer.or.jp)より)
文章問題は最優先で選択
文章の選択問題は簡単な問題がほとんどです。得点源です。
勉強するまでもないような常識問題もあります。
知識がない分野でも、過去問の引用や類似問題が多くあるので、過去問を繰り返し解き、暗記しましょう。
捨て問題を見極める
2群は他の群と比べると、難解な問題が少ないです。
ですが、聞いたこともないような単語や式、見たこともないような問題が出てきた場合は捨てる判断も必要です。
これは2群に限らず、基礎科目では共通の戦略となります。
というのも、そもそも技術士第一次試験は満点を目指す試験ではなく、5割以上とれれば合格する試験です。
過去問の類似問題や比較的簡単な問題も含まれている以上、解答を読んでも全く理解できないような問題を大学の参考書やインターネットで調べてまで理解しようとする必要ははっきり言ってありません。
捨て問題は7年分の過去問を3回繰り返せば自然と見極められるようになります。
過去問をこなせば、いわゆる「新傾向問題」や「初見問題」のようなものは見た瞬間にそう感じます。
本試験の際は、そのような問題を早々に飛ばし、他の問題に取り組むという素早い判断が必要です。



特に基礎科目は3科目のうち圧倒的に試験時間が厳しく設定されています。時間との勝負になりますので、難解な問題や新傾向問題を見極める力
をつけましょう。
参考までに、2群における下記の分野は、大学で専攻していた方や実務で精通している方以外は「捨て問題」にしていい問題の候補です。市販されている基礎科目の問題集などでも、難解な問題とされることが多い分野です。
- ユークリッド互除法
- 行列(頻出ではないため、わざわざ勉強し直すくらいなら捨てる)
- 写像(式を知らないと解けない)
- 漸近的記法
2群の目標得点


2群は難解な問題が出る可能性が低く、得点源にすべき分野です。
・文章問題で確実に1点を確保
・その他の問題で1点を確保
→ 2得点/3問 を目標とする。
稀にある難解な問題を見極め適切に避けることができれば、3点満点も難しくありません。
まとめ
本記事では技術士第一次試験 基礎科目のうち、2群(情報・論理)に特化して解説をしました。
2群は難解な問題が少なく、得点源を目指す分野です。
過去問を繰り返しこなし、合格を目指しましょう。






