こんにちは、ぱぱけん (@yi_ki411) です。
本記事では技術士第一次試験の基礎科目のうち、3群(解析に関するもの)に特化して出題内容の解説や勉強方法についてまとめています。
・基礎科目 3群の出題内容が知りたい
・3群の勉強方法と対策が知りたい
・3群の目標点を知りたい

技術士第一次試験に一発合格した筆者(@yi_ki411) が解説します。








3群の出題内容


まずは3群の出題内容を見てみましょう。
出題分野と問題形式
技術士第一次試験の基礎科目は「科学技術全般にわたる基礎知識」とされています。
その中でも3群は「解析に関するもの」という分野から出題されます。
各群で共通ですが、6問出題され、3問を選択し解答します。
3群では主に数学・物理の基礎問題が出題され、計算問題が多く出題されます。
数学・物理に関する出題内容は高校~大学レベルのものです。高校で数学ⅢCを習っていなかったり、大学で数学の授業を専攻していなかったりすると全くわからない問題も多いと思います。
このような方にとっては3群が基礎科目の中で最も得点が難しい分野となり、合格を左右する群になるといっても過言ではありません。
逆に、数学・物理を大学まで専攻していたり実務で多用している人にとっては得意分野になり、そういった意味で差が出る群と言えます。
高校数学で学ぶ「微分方程式」、「ベクトル」、「行列」に関する問題は頻出ですので、「習ってはいたけれど忘れてしまっている」という方は少し復習すれば解ける問題もあるはずです。
過去7年の出題内容
過去7年の2群の出題内容は下記のようになっています。
| 番号 | 令和4年度 | 令和3年度 | 令和2年度 | 令和元年度再 | 令和元年度 | 平成30年度 | 平成29年度 |
|---|---|---|---|---|---|---|---|
| 1 | 差分表現 | ベクトル解析 | ベクトル解析 | 微分方程式 | ベクトル解析 | 定積分 | 差分表現 |
| 2 | ベクトル解析 | 積分 | ベクトル解析 | ベクトル解析 | ヤコビ行列 | ベクトル解析 | ベクトル解析 |
| 3 | 誤差 | 有限要素法 | 誤差 | 有限要素法 | 流体速度 | 行列解析 | 有限要素法 |
| 4 | 弾性力学 | 弾性力学 | 面積座標 | 積分公式 | ポアソン比 | 非線形方程式 | 合成抵抗 |
| 5 | 角加速度 | 弾性力学 | 固有振動数 | 固有振動数 | 弾性力学 | 弾性力学 | 弾性力学 |
| 6 | 固有振動数 | 重心座標 | 管路の水の流れ | 楕円の応力状態 | 固有振動数 | 弾性力学 | 材料力学 |
表のうち青字で示したものは計算問題です。
3群の出題キーワード


3群の出題内容をキーワードで見てみましょう。
数学の分野と物理の分野に分けて整理します。
数学分野のキーワード
・偏微分方程式
・ベクトル解析
・発散
・勾配
・行列解析
・有限要素法
・誤差
物理学分野のキーワード
・材料力学
・弾性力学
・ヤング率
・フックの法則
・固有振動数
・流体力学
3群の勉強方法と対策


冒頭に述べた通り、3群は予備知識がないと基礎科目の中で最も対策が難しい分野となります。
そのため、戦略的に対策をする必要があります。
本章ではそのような予備知識がない方向けに、勉強方法と対策について具体的に解説をします。
しかし、



そんな私でも本番は3群で満点をとっています!(運もありますが・・・)
・捨て問題を早々に決め、学習方針を立てる
・最小限の基礎勉強をする分野を絞る(すべての分野を理解・対策しようとしない)
以上の2点が重要となります。
偏微分方程式
技術士第一次試験の偏微分方程式は実は非常に簡単な問題が多いです。
私も最初に問題を見たときはチンプンカンプンでしたが、少し高校数学の復習をして過去問をこなしたら解けるようになりました。
あなたは次の簡単な3次方程式について、xについて微分ができますか?
$$y=ax^{2}+bx+c$$
これがすんなり解ける方は技術士第一次試験の偏微分方程式の問題もほぼ解けます。
「1階偏微分」は微分を1回する、「2階偏微分」は微分を2回する、あとは微分しようとする符号がなにかという点に気を付けるだけです。



こんなざっくりした解説では数学専攻の方には怒られるかもしれませんが・・・
ベクトル解析と行列解析
少し復習して思い出せる方は積極的に勉強して下さい。
ただ、私は完全に捨てていました。
高校で習ってはいましたが、ベクトルと行列は覚えなければいけない基本式や式変形が多く、それを一から再習得するには時間がかかることから、割り切って何も対策をしませんでした。
過去問を見ると、ベクトル・行列に関連する出題は難解な問題も少なくないというのも早々に捨て判断をした理由のひとつです。
もちろん、解説を読んで理解できるレベルの方は前向きに取り組みましょう。
発散・勾配
ベクトル解析の問題で「直交座標」や「ベクトル」という文言とともに出題されますが、実は微分計算ができれば比較的簡単に解けます。
微分方程式を解ける方は解説を読めば理解ができるはずです。
ただし、三角関数のsinとcosが座標に出てきた場合、sinとcosの微分公式を知らなければ解けません。基本式を暗記しなければいけないため、式の暗記をしたくなければ三角関数が絡む場合は捨てる手もありでしょう。
有限要素法
解析をしたい対象を有限な要素に分解したものの集合体とみなし、各要素ごとに解析を行い全体の挙の近似値を求める方法で、数値解析手法のひとつ。
実務ではFEM(Finite Element Method)と略して呼ばれることが多い。
建築分野においては構造解析などで多用されます。
また、地盤工学、流体力学、電磁気学などの分野でも使われており、多方面で使われている解析手法です。
基礎科目 3群では、有限要素法に関する文章問題(正誤問題)が頻出です。
有限要素法について覚えるべきポイントは下記です。
・解析精度を上げるには、要素分割をできるだけ細かくする。
・要素分割が粗いと誤差が大きくなる。(応力や変位が小さく出たり大きく出たりする。)
誤差
基礎科目 3群において「誤差」といったら、数値解析における誤差のことを指します。
誤差には、丸め誤差、打切り誤差、桁落ち、情報落ち などがあり、それぞれ違った意味の誤差です。
各定義の違いを覚えておきましょう。
基礎科目 3群では、文章問題(正誤問題)として出題されます。
特に、「丸め誤差」が頻出です。
数値解析において、端数処理(四捨五入、切り上げ、切り下げ、丸めなど)をしたときに生じる誤差のこと
材料力学と弾性力学
材料力学とは、ある材料に力(荷重)が加わった時の変形や破壊について、数学的に求められる理論値と実験的に求められる経験値の両面から研究・評価を行う学問分野です。
弾性力学とは、「弾性体」と定義される物体に関して、材料力学の考え方を基礎として、さらに「弾性」の概念を取り込んでいます。
「弾性」とは「力が加わると変形を生じ、その力がなくなると元に戻る」性質のことです。
弾性力学はこのような物体(=弾性体)を取り扱う力学で、材料力学における「応力」に加えて、「変形(=ひずみ)」の概念をもつことが特徴です。
このように、工学分野によって意味合いが違うために定義が曖昧な部分もありますが、技術士第一次試験においてはその定義や違いよりも、概念や考え方、基本式をおさえることが重要となります。
基礎科目 3群では材料力学・弾性力学に関する問題がほぼ毎年出題されており、超頻出の分野です。
合格のために避けては通れないことはもちろんですが、技術者にとって当然理解しておくべき分野であるため、毛嫌いせずにしっかりと勉強をしましょう。
ここでは、材料力学と弾性力学に関する出題ポイントを解説していきます。
ヤング率とフックの法則
「力が加わると変形を生じ、その力がなくなると元に戻る」性質をもつ弾性体は、弾性を示す範囲(弾性域)において、応力σとひずみεが比例関係にあります。
このときの比例定数を弾性率Eといいます。
特に、一方向応力に対する変形(伸び・縮み)の場合、弾性率Eのことをヤング率Eといいます。
これを式で表すと、
$$σ=Eε$$
となります。
この式を「フックの法則」といいます。
技術士第一次試験では必ず必要になる式ですので、暗記して下さい。
同じ応力ではひずみが小さいほうが、同じひずみでは応力が大きいほうがヤング率は大きくなります。つまり、ヤング率というのは「変形のしにくさ」を表しています。
注意点として、「ひずみε」は「変形量」ではありません。
元のLに対する変形量ΔLの比率です。
$$ε=ΔL/L$$
と表します。
式を見ても明らかなように、ひずみεは無次元量になります。
応力σとは
「応力」とは、外力が加わった材料の内部に生じる力(=内力)のことです。
材料力学で「応力」として説明しているものは、厳密には「応力度」のことです。
建築・土木の構造力学分野では「応力」と「応力度」は明確に区別して使われます。
応力は「内力」 単位は[N]または[kN]など
応力度は「単位面積当たりに生じる応力」 単位は[N/mm2]または[kN/m2]
フックの法則における応力σは、単位は[N/mm2]であり、構造力学分野における応力度のことを指します。
応力は3種類あります。
①軸方向力(圧縮・引張)
②せん断力
③曲げモーメント
それぞれ「応力度」で表現でき、部材の許容応力度以内であることを確認する構造設計手法が「許容応力度設計」です。
技術士第一次試験では、応力度の定義とフックの法則を覚えておくだけで解ける問題が頻出となっています。
必ずマスターしましょう。
固有振動数
すべての物体は固有の振動数(1秒間に振れる回数)を持っており、これを「固有振動数」といいます。
物体の振動といっても、何種類かあります。
技術士第一次試験では下記の3種類が出題されます。
質量系の振動です。
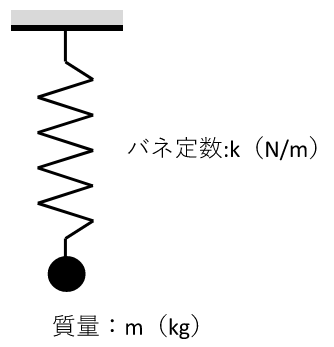

固有振動数 $$f=\frac{1}{2π}\sqrt{ \frac{k}{m} }$$
単位:[Hz]
糸に吊らされた質量系の振り子振動です。
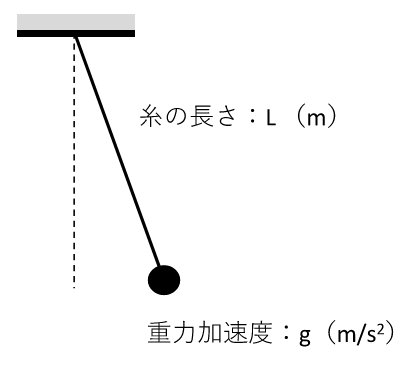

固有振動数 $$f=\frac{1}{2π}\sqrt{ \frac{k}{m} }$$
単位:[Hz]
たわみを生じる「はり」の振動です。


固有振動数 $$f=\frac{1}{2π}\sqrt{ \frac{g}{δ} }$$
単位:[Hz]
固有振動数の公式は暗記して下さい。
固有角振動数は、
$$ω=f×2π$$
と覚えておきましょう。
流体力学
管路を流れる水や流体に関する問題が出題されます。
超頻出というわけではありませんが、公式を覚えておくだけで比較的簡単に解けるので、余裕があれば対策をしておきたいです。
ポイントは下記の2点です。
①同一の管路内の「流量」は一定である。
②管路の断面積が一定であれば、流体の速度も一緒である。
式で表すと、
$$Q=v・A=一定$$
となります。
また、「ベルヌーイの定理」という重要な公式があります。
$$\frac{v^2}{2g}+z+\frac{P}{ρg}=一定$$
第一項:速度水頭
$$\frac{v^2}{2g}$$
第二項:位置水頭
$$z$$
第三項:圧力水頭
$$\frac{P}{ρg}$$
を意味します。
「速度水頭、位置水頭、圧力水頭の総和は常に一定」という意味です。
エネルギー保存則のイメージで覚えましょう。
流体力学自体が建築分野に従事する方にとって馴染みがない分野かと思いますが、Q=v・Aとベルヌーイの定理だけ覚えていれば基礎科目の問題は解けます。
また、建設部門を受験する方は、専門科目でベルヌーイの定理を使う問題があります。ほぼ避けては通れないというつもりで、これを機に勉強することをおすすめします。
捨て問題とする分野を早々に決める
3群は予備知識がない場合、対策に時間がかかります。
数学・物理の基礎知識を一から勉強するのは容易なことではありません。
一方で、技術士第一次試験は満点を目指す試験ではなく、5割以上とれれば合格する試験です。
3群に時間を割くよりも、その他の群の解ける問題を増やすほうが得策です。
捨てる分野・捨てる問題を早々に決め、割り切って勉強をしないというのが合格への近道です。
3群の目標得点


繰り返しになりますが、これまで述べてきたような数学と物理の基礎に関する予備知識がない方にとって、3群は基礎科目の中でも一番難しく対策がしづらい群となります。
一から習得するには時間のかかる学問分野もあり、あまり時間をかけすぎるのも基礎科目対策としては得策ではありません。
そのような方は3群で1点を目標とし、他の群で得点を確実にとるという戦略がよいでしょう。
まとめ
本記事では技術士第一次試験 基礎科目のうち、3群(解析)に特化して解説をしました。
3群は対策が難しい群であり、戦略的な学習方針を立てることが重要です。
過去問を繰り返しこなし、合格を目指しましょう。






